Proyecciones ortogonales
la proyección ortogonal es aquella cuyas rectas proyectantes auxiliares son perpendiculares al plano de proyección (o a la recta de proyección), estableciéndose una relación entre todos los puntos del elemento proyectante con los proyectados.
- Proyección ortogonal de un punto
- La proyección ortogonal de un punto P en una recta L es otro punto A que se obtiene trazando una línea auxiliar perpendicular a L desde el punto A tal que esta línea pase por P. Lógicamente, si el punto P pertenece a la recta L, coinciden: P = A .
- Proyección ortogonal de un segmento
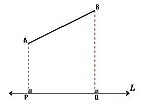
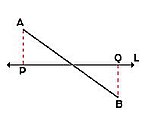
- Caso general: si el segmento dado AB no es paralelo a la recta L, la proyección ortogonal es un segmento PQ que se obtiene trazando líneas perpendiculares a L desde los puntos extremos de AB. La magnitud de la proyección siempre es menor que la del segmento dado.
- Si el segmento PQ y la recta L son paralelos, la proyección será: AB = PQ, que se obtiene de forma análoga.
- Si el segmento AB tiene un punto común con la recta L, la proyección se obtiene de modo similar.
- Si el segmento AB corta a la recta L, la proyección se obtiene de forma análoga.
- Definicones
- Proyeccione es el resultado de proyectar, un verbo que se refiere a guiar algo hacia adelante, planificar o lograr que un objeto sea visible sobre la figura de otro. Ortogonal , por su parte, es lo que se encuentra en un ángulo de noventa grados.
-
Una proyección ortogonal, por lo tanto, es aquella que se crea a partir del trazado de la totalidad de las rectas proyectantes perpendiculares a un cierto plano. De este modo, existe un vínculo entre los puntos de aquello que se proyecta con los puntos proyectados.
Lo que posibilita la proyección ortogonal es el dibujo de un mismo objeto, que se encuentra en el espacio, en planos diferentes. De este modo, el resultado es la posibilidad de contar con dos o más puntos de vista distintos del objeto en cuestión.
Para conocer completamente las características de un objeto no basta con dibujarlo desde una posición determinada, sino que hay que realizar varias representaciones desde distintos puntos de vista. Así, si observamos un dibujo de una iglesia obtenido mirando su fachada, no podemos saber cómo es su planta, cómo son sus laterales, etc.Para obtener las proyecciones ortogonales de un objeto se dan los siguientes pasos.- 1. Se sitúa el objeto de forma que sus caras sean paralelas o perpendiculares al plano del papel.
- 2. Se observa el objeto de forma que las líneas visuales pasen por sus vértices, incidiendo perpendicularmente sobre el plano de proyección, tal y como muestra la figura de la derecha.
- 3. Para obtener el alzado, se elige el punto de vista que permita observar más detalles del objeto. Por ejemplo, en un coche, una vista desde el frente.
- 4. Para obtener la planta, se gira 90º hacia arriba respecto a la posición anterior. En el caso de un coche, la planta se obtendría mirando el coche desde arriba.
- 5. Por último, para obtener el perfil, se parte de nuevo de la posición desde la que se ha obtenido el alzado y se gira 90º hacia la izquierda. En un coche, el perfil coincidiría con la vista desde un lateral.
Definición de traslaciones
Las traslaciones pueden entenderse como movimientos directos sin cambios de orientación, es decir, mantienen la forma y el tamaño de las figuras u objetos trasladados, a las cuales deslizan según el vector. Dado el carácter de isometría para cualquier punto P y Q se cumple la siguiente identidad entre distancias:
Más aún se cumple que:
Notas:
- La figura trasladada es idéntica a la figura inicial.
- La figura trasladada conserva la orientación que la figura original.
- (también llamada rotacional, radial o cilíndrica) es la simetría alrededor de un eje, de modo que un sistema tiene simetría axial o axisimetría cuando todos los semiplanos tomados a partir de cierto eje y conteniéndolo presentan idénticas características
La simetría axial se da cuando los puntos de una figura coinciden con los puntos de otra, al tomar como referencia una línea que se conoce con el nombre de eje de simetría. En la simetría axial se da el mismo fenómeno que en una imagen reflejada en el espejo.
SIMETRÍA AXIAL DE UN TRIANGULO
ROTACIÓN DE FIGURASRotación es el movimiento de cambio de orientación de un sólido extenso de forma que, dado un punto cualquiera del mismo, este permanece a una distancia constante del eje de rotación. Una rotación pura de un cuerpo queda representada mediante el vector velocidad angular, que es un vector de carácter deslizante,
 situado sobre el eje de rotación.
situado sobre el eje de rotación.
Puesto que a la rotación también se le llama, erróneamante, revolución, debemos diferenciar claramente el significado de estos términos.
- La rotación de un cuerpo alrededor de un eje
(exterior o interior al cuerpo) corresponde a un movimiento en el que
los distintos puntos del cuerpo presentan velocidades que son
proporcionales a su distancia al eje. Obviamente, los puntos del cuerpo
situados sobre el eje (en el caso de que este sea interior al eje)
permanecen en reposo.
- La orientación del cuerpo en el espacio cambia continuamente durante la traslación.
- Un ejemplo de rotación el de la Tierra alrededor de su propio eje de rotación, con un periodo de rotación de un día sidéreo.
- La rotación de un cuerpo alrededor de un eje
(exterior o interior al cuerpo) corresponde a un movimiento en el que
los distintos puntos del cuerpo presentan velocidades que son
proporcionales a su distancia al eje. Obviamente, los puntos del cuerpo
situados sobre el eje (en el caso de que este sea interior al eje)
permanecen en reposo.